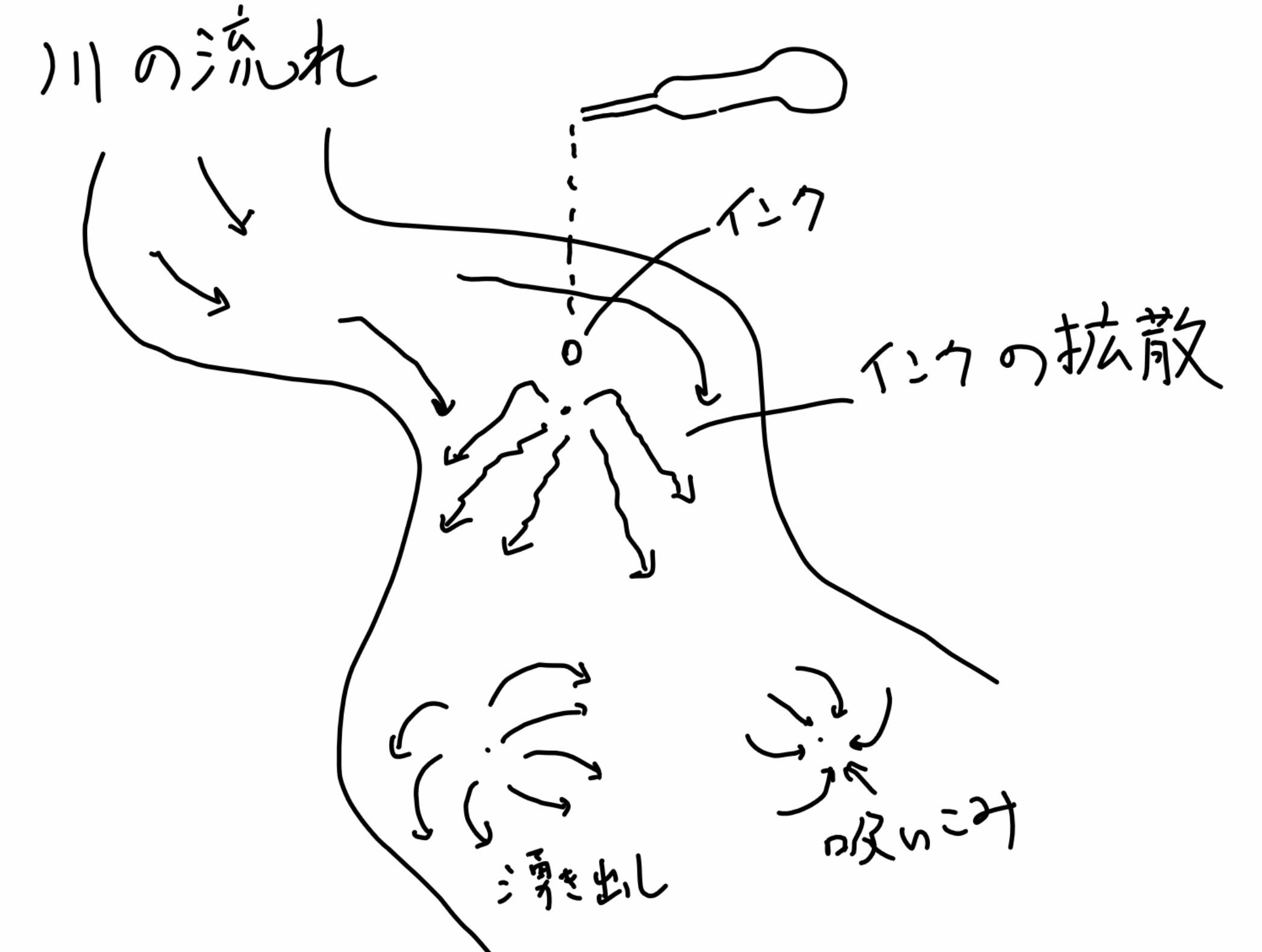
数学では「存在することはわかるが、具体的な形はわからない」という主張に出会うことがよくあります。表題の「川に垂らしたインクがどのように拡散していくか」という問題も拡散方程式の一般論から適切な仮定の下で解が一意的に存在することは証明できるのですが、川がくねくねと曲がっていたり、水の出入りがあるような複雑な流れの場合はインクが具体的にどのように広がっていくのかを決定することは大変難しい問題です。
私は最近出版された慶應義塾大学の河備浩司教授との共著論文において、この問題の1つの解決方法として、川を細かい部分に分割して離散化し、この離散モデル上の離散的な方程式の解でインクの分布が近似できることを示しました。近年,計算機の性能が飛躍的に上がったことにより、このような問題でも解の離散近似が容易に求められるようになってきましたが、近似解が実際の解をちゃんと近似していることを保証する基礎理論が背後で重要な役割を果たしています。
准教授 石渡 聡(理学部 確率論と幾何学)


寄附・研究のお申し込みはこちら
いいね
0
会員ログイン